[:en]The latest paper with Kimara Naicker and Ilya Sinayskiy was just published in Physical Review Research.
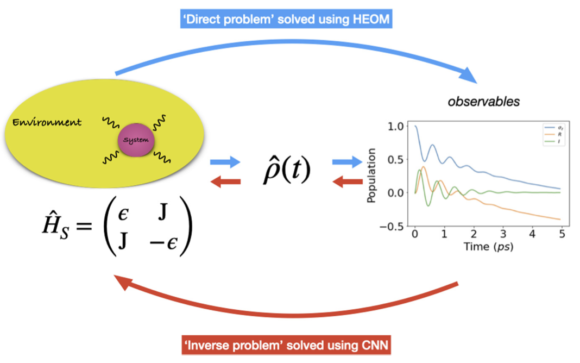
Abstract: A wellknown approach to describe the dynamics of an open quantum system is to compute the master equation evolving the reduced density matrix of the system. This approach plays an important role in describing excitation transfer through photosynthetic light harvesting complexes (LHCs). The hierarchical equations of motion (HEOM) was adapted by Ishizaki and Fleming [J. Chem. Phys.130, 234111 (2009)] to simulate open quantum dynamics in the biological regime. We generate a set of time-dependent observables that depict the coherent propagation of electronic excitations through the LHCs by solving the HEOM. The computationally intractable problem here is addressed using classical machine learning (ML). The ML architecture constructed here is of model character and it is used to solve the inverse problem for open quantum systems within the HEOM approach. The objective is to determine whether a trained ML model can perform Hamiltonian tomography by using the time dependence of the observables as inputs. We demonstrate the capability of convolutional neural networks to tackle this research problem. The models developed here can predict Hamiltonian parameters such as excited state energies and inter-site couplings of a system up to 99.28% accuracy.
Reference: Kimara Naicker, Ilya Sinayskiy, and Francesco Petruccione, Machine learning for excitation energy transfer dynamics, Phys. Rev. Research 4, 033175 – Published 6 September 2022
The pdf can be downloaded from here
[:]
